Understanding Transcendental Numbers: Their Role in Mathematics, AI, and Quantum Computing

Transcendental numbers are a class of real or complex numbers that are not algebraic.

Mar 17, 2025

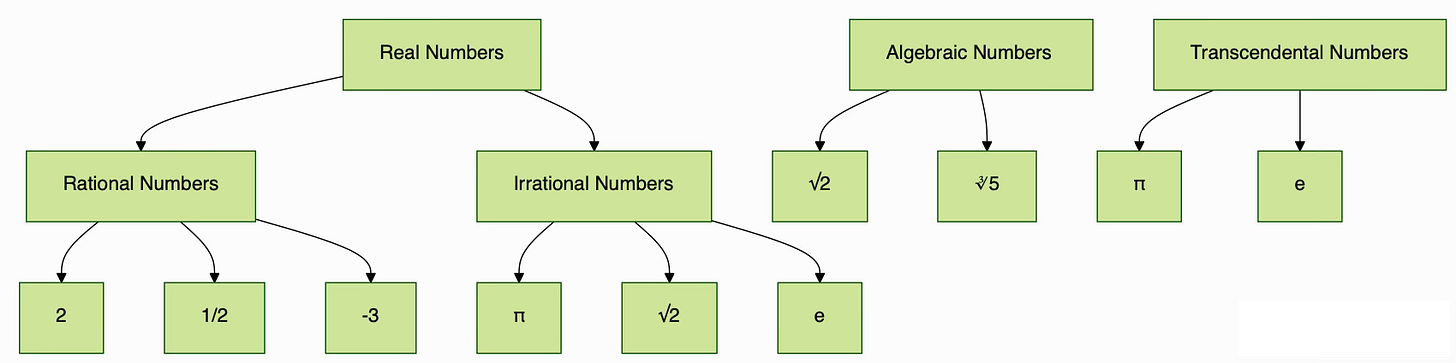
Transcendental numbers are a captivating topic in mathematics, forming a unique subset of numbers with profound implications in various fields, including Artificial Intelligence (AI) and Quantum Computing. To appreciate their significance, it is essential to first understand the broader classification of numbers.

Types of Numbers

The number system is divided into several categories:

Natural Numbers : These are the basic counting numbers, such as
$1, 2, 3, \dots$
.
denoted by the symbol
$\mathbb{N} $
Integers: These include all whole numbers, both positive and negative, as well as zero.
denoted by the symbol
$\mathbb{Z}$
Rational Numbers : Numbers that can be expressed as a fraction
$\frac{p}{q}, \text{where } p \text{ and } q \text{ are integers and } q \neq 0.$
denoted by the symbol
$\mathbb{Q} $
Irrational Numbers: Numbers that cannot be expressed as a fraction of two integers.
$e.g., \sqrt{2}, \pi$
Real Numbers : All numbers that can be represented on the number line, including both rational and irrational numbers.
denoted by the symbol
$\mathbb{R} $
Complex Numbers : Numbers of the form
$a + bi, \text{where } a \text{ and } b \text{ are real numbers and } i \text{ is the imaginary unit with } i^2 = -1.$

denoted by the symbol

$\mathbb{C} $

Within this hierarchy lies a special class of numbers known as transcendental numbers.

What Are Transcendental Numbers?

Transcendental numbers are real or complex numbers that are not algebraic. A number is algebraic if it is a root of a non-zero polynomial equation with rational coefficients.

$\text{For example}, \sqrt{2} \text{ is algebraic because it satisfies the equation: } x^2 - 2 = 0 $

In contrast, transcendental numbers do not satisfy any such polynomial equation. Famous examples include

$\pi \text{ (the ratio of a circle's circumference to its diameter)} $

$e \text{ (the base of natural logarithms)}$

These two constants have been rigorously proven to be transcendental.

Properties of Transcendental Numbers

Irrationality: All transcendental numbers are irrational, but not all irrational numbers are transcendental.
$\text{For instance,} \sqrt{2} \text{ is irrational but not transcendental.}$
Operations with Algebraic Numbers: If you add, subtract, multiply, or divide an algebraic number (except zero) by a transcendental number, the result is still transcendental.
Non-Periodic Nature: Transcendental numbers often appear in contexts involving non-repeating or non-periodic phenomena.

Mathematical Applications of Transcendental Numbers

Exponential Functions in Neural Networks

In AI, transcendental functions like the exponential function play a key role in neural network activation functions. For instance, the softmax function normalizes outputs into probabilities:

$\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}} $

$\text{Here,} e^{x_i} \text{ involves the transcendental constant $e$. }$

This function ensures that the output values lie between 0 and 1, making them interpretable as probabilities

Quantum Phase Estimation

In quantum computing, transcendental numbers appear in operations involving rotations of quantum states.

$\text{For example, the rotation operator around the } z-axis \text{ by an angle } \theta \text{ is given by: } R_z(\theta) = \begin{pmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{pmatrix} $

Here, the exponential terms involve complex powers of e, which are deeply tied to transcendental mathematics.

Quantum Fourier Transform

The Quantum Fourier Transform (QFT), a cornerstone algorithm in quantum computing, also relies on transcendental functions.

$\text{The QFT transforms a quantum state } \lvert x \rangle \text{ into another state using: } QFT_N \lvert x \rangle = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2\pi i xy / N} \lvert y \rangle $

$\text{The exponential term } e^{2\pi i xy / N} \text{ involves } \pi$

which is transcendental. This transformation allows for efficient computation of periodicity in quantum systems.

Error Analysis in AI Models

Transcendental functions like sine and cosine are also used in error analysis and optimization algorithms for AI models. For example, when calculating root mean square error (RMSE):

$\text{Error} = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2} $

The square root function itself is closely related to exponential functions via fractional powers.

Why Are Transcendental Numbers Important?

Transcendental numbers represent phenomena that cannot be captured by simple polynomial equations. They appear naturally in contexts involving growth rates (like population or radioactive decay), wave mechanics (sine and cosine), and geometry (circle measurements). Their prevalence in AI and quantum computing underscores their importance in modeling real-world systems and solving complex computational problems.

For instance:

In AI, they enable smooth activation functions critical for gradient-based optimization methods.
In quantum computing, they allow precise manipulation of quantum states for algorithms like Shor's factoring or Grover's search.

Conclusion

Transcendental numbers are more than just mathematical curiosities; they serve as fundamental tools for understanding and solving problems in advanced fields like AI and quantum computing. Their intrinsic connection to exponential growth, waveforms, and rotations makes them indispensable for modeling both natural phenomena and computational processes. As we continue to push the boundaries of technology and mathematics, the study of transcendental numbers will remain an essential part of our journey into the unknown.

VMacWrites

Discussion about this post